The Precision Loss of Ballscrew with Short-Time Overload Impact

Ball screw is the driving utilitarian component most as often as possible utilized for the exactness hardware. To a certain degree, the transmission precision of exactness gear is influenced by the position blunder of ball screw caused by the elastic– plastic distortion between ball and raceway beneath the over-burden affect. This article points to examine the exactness misfortune of ball screw considering short-time over-burden affect. A novel exactness misfortune show combining the Hertzian and Thornton contact hypotheses is set up to depict the varieties within the pivotal distortion profundities. In this way, the pivotal precision misfortune can be characterized as the differential esteem between the beginning no-loading travel varieties and the stacking stroke varieties caused by the pivotal plastic distortion of raceway. In the interim, the greatest push and the remaining plastic distortion for four couples of ball-raceway materials are analyzed. Moreover, the relationship between the precision misfortune and the elastic–plastic distortion for four couples of ball-raceway materials are analyzed. Moreover, the relationship between the precision misfortune and the elastic–plastic distortion is examined by the hypothetical investigation and tests. The comes about appear that the position and accuracy is influenced in fact by the contact mishapening. The position and accuracy misfortune of the nut relative to the screw increments with the increment within the pivotal stack. The results can offer assistance to supply the expectation for the precision life of ball screw working in high-load condition.

With the advancement of the extraordinary hardware manufacturing industry, such as highload and high-precision hardware, the high-reliability center transmission parts are basic specialized challenge for the expansive gear. Within the fast advancement of the aviation defense attempt and deep-sea operation gear, the transmission framework with ball screw is influenced by the deep-sea tall weight and the affect working conditions, such as the docking of shuttle, the opening and closing of the carry cabin entryway, the spreading and withdrawing of air ship landing equip, and the swing of the deep-sea mechanical arm. In this way, the necessities are displayed on the bearing capacity, affect resistance, exactness sustainability, and execution reliability of ball screw within the particular transmission framework. The equivalent elastic Hertz stresses are a common approach for the static load rating determination of ball bearings in all bearing industries. This theory can be used to determine the limit equivalent static stress for elastic contact stress between two curved bodies. The Hertzian contact mechanism gives an accurate non-linear model for the elastic contact problem of two different bodies, which is the basis for analyzing the elastic–perfectly plastic contact problem. The elastic approach (deformation) of ball screw in the contact points can be obtained .

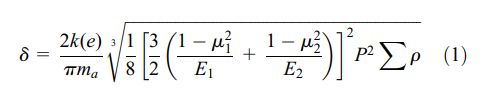
where r is the sum of principal curvature; ma is the coefficient of semi-major axes of contact ellipse; d is the contact deformation between the ball and the raceway; k(e) is the eccentricity of ellipse; P is the normal contact force; E1 and E2 are effective Young’s moduli of two different contact surfaces, respectively; and m1 and m2 are effective Poisson’s ratio of two different contact sur- faces, respectively. The contact between two general contact bodies with four different curvature radii has to be considered. The contact stress distribution of the full contact surface can be obtained as follows.

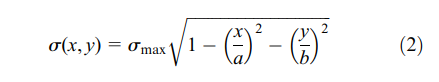
where a and b are the semi-major axis and the semi-minor axis on the contact ellipse, respectively. The maximum stress can be expressed as

The elastic deformation loading formula can be obtained by equation (1)

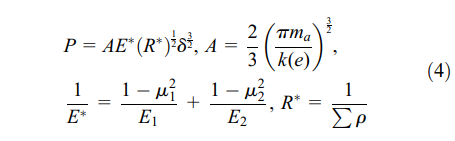
where A is the coefficient of deformation, E* is the equivalent Young’s modulus, R* is the reciprocal value of the sum of the principal curvature, and ma is the coefficient of semi-major axes of contact ellipse. The contact elliptical area can be obtained

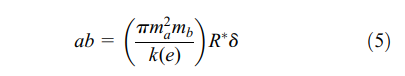
When the contact area of ball screw subjected to the normal load is to yield, the semimajor axis and the semi-minor axis of the contact ellipse are a = as and b = bs, respectively. And, smax = ss/(1.73 * kst) is obtained based on the von Mises yield criterion, where kst is the assurance coefficient dependent on material properties. By substituting equations (4) and (5) into equation (3).